SRAS for materials characterisation
What is SRAS
|
|
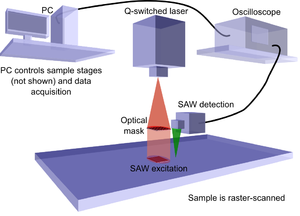
SRAS stands for Spatially Resolved Acoustic Spectroscopy, it is a technique for mapping the surface acoustic wave velocity of a material. The technique is analogous to optical spectroscopy techniques where analysis of the optical spectrum and the wavelengths that are most readily transmitted or absorbed tells us some properties of the sample being examined. In the acoustic sense we monitor the spectrum of sound waves emitted from a grating source. The technique can be performed two ways, the first is to use a fixed frequency source and sweep the grating spacing or the grating period can be fixed and the frequency is swept.
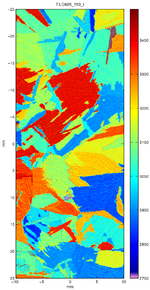
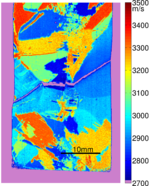
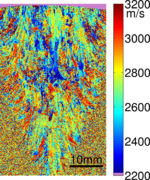
To measure the acoustic spectrum at each point on the sample a fixed grating is illuminated with a short laser pulse (typically ~1ns). As the laser pulse contains a broad range of frequencies, only the frequencies which match the grating spacing and acoustic velocity of that sample point will be generated. We measure the waves that have been generated close to the excitation region (see top figure). We can then calculate the frequencies generated and with the knowledge of the grating spacing we can obtain the acoustic velocity using v = fλ. If the sample is raster scanned we build up a detailed image of the sample velocity for that propagation direction. These images show the grain structure of the material and are very useful for material scientists for assessing the properties of the material.
EMDA Sponsored Instrument

|

|
The EMDA instrument is the most advanced version of SRAS instrumentation we have at Nottingham. This instrument has been developed to provide rapid velocity imaging on a variety of surface finishes.
The instrument uses a fixed grating, projecting a pattern of stripes onto the sample. These stripes define the wavelength of the generated acoustic waves. The mask is illuminated with a short pulse of laser light ~1ns, the mask acts as a filter and so only sound waves with the frequency to match the fixed wavelength and the velocity of the material under the patch are generated. We detected the generated waves close to the generation region. We determine the velocity by looking at the frequency of the waves we detect and our knowledge of the mask spacing.
This approach allows the determination of the velocity for each laser pulse. This makes the data acquisition very fast. The laser in the EMDA system fires 6000 times a second, so we can take 6000 velocity measurements per second. Real scanning rates, which include the movement of stages, data downloading etc, reduce this rate to ~1200 points/second. This is 100 times faster than previous generations of the instrument.
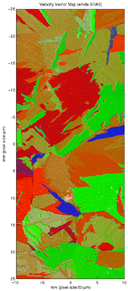
The EMDA instrument can also generate waves in any arbitrary direction by rotating the mask pattern The detection spot can also be moved by use of a computer controlled mirror. this allows for velocity surface measurements or velocity vector maps to be produced with the need to rotate the sample. The instrument is being upgraded to cope with optically rough surfaces which will allow scanning to take place on more industrially relevant samples.
The instrument has exceptional spatial resolution and operating frequency range. Routine scans have been performed from 100-300 MHz with spatial resolution better than 50 microns/pt. With this resolution it is possible to see very fine details in material structure.
All these capabilities have been constructed into a compact head that can be mounted above a scanning system, as picutred, or mounted directly to a scanning head. The dimensions are approximately 350x200x150 mm with an umbilical connection to a rack containing the computer and other electronics.
From Velocity to Orientation
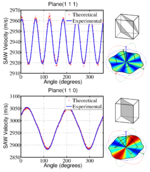
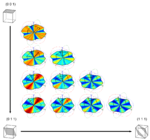
To provide orientation measurements we need to convert from velocity contrast maps to true orientation information. The acoustic velocity of a known material in a known orientation can be calculated analytically. We use a method outlined by Farnell. This method is used to calculate SAW and pseudo-SAW velocities on different crystallographic planes by using iterative search procedures and the known materials' elastic constants. The method requires the iteration through different SAW velocities in a specified range to find out which velocities satisfy the boundary conditions. Using this method we can calculate the velocity surface for any crystallographic orientation..
The output from the model gives us an idea of w which wave modes e.g. surface waves, pseudo surface waves and leaky modes that may propagate for that orientation. We have to work out which of these our experiment will be sensitive to and that depends on he type of detector used. for example our current detector is sensitive only to the out of plane motion of the waves, so we calculate the out of plane motion for all of the modes found during the search and choose the dominant mode. This then gives us an indication of the expected velocity surface for that crystallographic orientation that will be measured with our experiment.
To find an orientation from experimental data we fit our experimentally obtained velocity surface to a database of velocity surfaces in all possible orientations until we get a good match.
History of the technique
description of k sras and older instruments